Nombre de reproduction de base

En épidémiologie, le nombre de reproduction de base ou ${\displaystyle R_{0}}$ (ratio 0) d'une infection peut être défini comme le nombre moyen attendu de cas directement générés par un cas dans une population où tous les individus sont sensibles à l'infection^[1],[2].

C'est un paramètre permettant de modéliser l'évolution d'une épidémie au fil du temps, en supposant que le facteur pathogène ne mute pas et que l'immunité acquise dure au-delà de la période épidémique.

Définition et propriété de base

${\displaystyle R_{0}}$ varie en fonction de trois facteurs principaux : la durée de la phase contagieuse, la probabilité d'une transmission de l'infection lors d'un contact, et le nombre moyen de contacts d'une personne contaminée. À cela peuvent s'ajouter, selon les modèles utilisés pour le déterminer, des facteurs socio-économiques et environnementaux, qui peuvent conduire à des estimations différentes de ce ${\displaystyle R_{0}}$^[3].

Croissance ou décroissance exponentielle

« Le ${\displaystyle R_{0}}$ [est] le nombre moyen de personnes qu’une personne contagieuse peut infecter^[4]. »

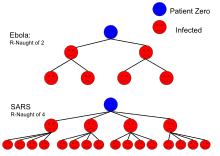
Supposons qu'un « patient zéro » se trouve d'une manière ou d'une autre en position de contaminer son environnement, le mécanisme de propagation de l'infection sera par hypothèse le suivant en moyenne :

• Au premier rang de transmission, ${\displaystyle R_{0}}$ individus seront infectés ;
• Ceux-ci étant à leur tour contaminants, chacun contaminera ${\displaystyle R_{0}}$ personnes, et donc au deuxième rang de transmission, ${\displaystyle (R_{0})^{2}}$ individus seront infectés ;
• Ceux-ci étant à leur tour contaminants, chacun contaminera ${\displaystyle R_{0}}$ personnes, et donc au troisième rang de transmission, ${\displaystyle (R_{0})^{3}}$ individus seront infectés ;
• ... ; et donc au n^ème rang de transmission, ${\displaystyle (R_{0})^{n}}$ individus seront infectés ; et ainsi de suite^[5].

Le nombre de personnes infectées varie donc exponentiellement.

Une propriété importante de ce ${\displaystyle R_{0}}$ est que :

• Si ${\displaystyle R_{0}>1}$, la croissance sera exponentielle, et l'épidémie va se propager. En général, plus la valeur de ${\displaystyle R_{0}}$ est grande, plus il est difficile de maîtriser l'épidémie ;
• Si ${\displaystyle R_{0}<1}$, la décroissance sera exponentielle et l'épidémie va s'éteindre.

Nombre de reproduction effectif

En réalité, le ${\displaystyle R_{0}}$ ne décrit l'évolution d'une maladie qu'à ses tout débuts.

« Ce taux s’applique, et se calcule à partir d’une population qui est entièrement susceptible d’être infectée, c’est-à-dire qui n’a pas encore été vaccinée ni immunisée contre un agent infectieux^[4]. »

Lorsqu'une fraction ${\displaystyle (1-f)}$ de la population a déjà été infectée ou est immunisée, les contacts avec cette fraction ne conduiront pas à des contaminations supplémentaires, et seule la fraction ${\displaystyle f}$ reste susceptible d'être contaminée. Dans ce cas, le nombre de reproduction effectif ${\displaystyle R}$ sera :

${\displaystyle R=f\cdot R_{0}}$

D'autre part, lorsque l'épidémie s'étend exponentiellement, la fraction ${\displaystyle f}$ diminue également exponentiellement, réduisant d'autant le ${\displaystyle R}$ effectif. Dans ce cas, pour des petites valeurs de ${\displaystyle R_{0}}$, on montre que la courbe de contamination est bien approchée par une courbe logistique. Au fur et à mesure qu'une fraction de plus en plus importante de la population est touchée, le ${\displaystyle R}$ effectif diminue et finit par devenir inférieur à l'unité : la vitesse de propagation diminue ; et à partir d'un certain point, c'est la décroissance qui devient exponentielle, et l'épidémie s'éteint d'elle-même^[6],[7],[8].

Seuil d'immunité collective

Le ${\displaystyle R_{0}}$ permet également de déterminer la proportion minimale au sein d'une population (${\displaystyle P}$) qui doit être immunisée par l’infection naturelle ou par vaccination (si disponible) pour empêcher le déclenchement ou la persistance d’une épidémie :

${\displaystyle P=1-{\frac {1}{R_{0}}}}$, ou encore : ${\displaystyle f={\frac {1}{R_{0}}}}$

On parle à ce propos d'effet d'immunité collective (immunité grégaire, herd immunity) pour désigner le pourcentage de la population qui devrait être immunisée pour que l’épidémie cesse de prospérer.

L'évolution d'une épidémie par rapport à ce point dépend du nombre de cas actifs. Quand ce point est atteint, la courbe de nouveaux cas passe par un maximum et commence à décroître. Ce n'est pas encore la fin de l'épidémie, mais le plus dur est passé.

Si cette proportion est présente dès le début d'une épidémie, par exemple à la suite d'une immunisation acquise lors d'une épidémie précédente, ou par une campagne de vaccination, alors l'épidémie sera étouffée dans l’œuf et ne pourra pas se développer.

Inversement, dans une situation d'endémie, pour laquelle le nombre de personnes affectées est relativement stable et le ${\displaystyle R}$ effectif proche de l'unité, la proportion ${\displaystyle f}$ de personnes n'ayant pas eu la maladie est égale à ${\displaystyle 1/R_{0}}$.

Ratio 0 et politique sanitaire

Mesures sanitaires

La modélisation de base est que, en moyenne, un individu infectieux établit ${\displaystyle \beta }$ contacts infectieux par unité de temps, pendant une période infectieuse moyenne de ${\displaystyle \tau }$. Le nombre de reproduction de base sera alors :

Cette durée ${\displaystyle \tau }$ est une donnée biologique de la maladie.

Afin d'estimer l'effet de cette politique sur le ${\displaystyle R_{0}}$, des hypothèses sont nécessaires sur le délai ${\displaystyle \delta _{d}}$ entre l'infection et le diagnostic, le délai ${\displaystyle \delta _{0}}$ entre l'infection et le début de la contamination, et la durée ${\displaystyle \delta _{c}}$ de la période contaminante. Si un diagnostic peut être posé avant même le début de la phase de contamination, et conduit à un isolement strict, il est clair que le ${\displaystyle R_{0}}$ sera réduit à pratiquement zéro, et l'épidémie sera stoppée net. Si le diagnostic est plus tardif, un isolement reste d'autant plus efficace qu'il est rapide et permet de réduire par l'isolement la durée ${\displaystyle \delta _{c}}$ de la période contaminante.

Mesures sociales

Le facteur ${\displaystyle \beta }$, en revanche^{[Information douteuse]}, est une donnée sociologique. Cette formule simple suggère différentes manières de réduire ${\displaystyle R_{0}}$, et finalement la propagation de l'infection. Il est possible de diminuer le nombre de contacts infectieux par unité de temps ${\displaystyle \beta }$ :

• en réduisant le nombre de contacts par unité de temps (par exemple rester à la maison si l'infection nécessite un contact avec les autres pour se propager) ;
• ou en réduisant la proportion de contacts qui produisent une infection (par exemple avec le port d'équipement de protection).

En isolant les deux facteurs précédents, le taux peut finalement être écrit de manière équivalente, sous la forme ^[9]

${\displaystyle R_{0}={\overline {c}}\,T\,\tau ,}$

où ${\displaystyle {\overline {c}}}$ est le taux de contact entre individus sensibles et infectés, et ${\displaystyle T}$ est la transmissibilité, c'est-à-dire la probabilité d'infection lors d'un contact.

Cette formulation est parlante, et permet de comprendre les différentes stratégies utilisées pour maîtriser une épidémie, mais est sans utilité pratique pour ce qui est des modélisations quantitatives de sa modélisation.

Effets d'une politique sanitaire

Une stratégie de prévention consiste à donner à la population concernée un ${\displaystyle R_{0}}$ a priori, tel que l'immunité collective est atteinte dès avant le début de l'épidémie, interdisant par là même un développement significatif.

• Sur le plan médical, le développement d'une stratégie adaptée de détection et de soins d'une maladie permettra d'augmenter l'efficacité générale du système de santé, réduisant a priori la durée ou la contagiosité de cette maladie^{[Information douteuse]}, et donc sa capacité à se transformer en épidémie ;
• Sur le plan de la politique de santé, une campagne de vaccination préventive peut amener la proportion de population immunisée au-dessus du seuil d'immunité collective ;
• Sur le plan social, la capacité d'une société à transmettre un agent pathogène peut être diminuée par l'éducation générale à des gestes réflexes d'hygiène (ne pas cracher par terre, se protéger la bouche quand on tousse…), réduisant dans l'absolu la proportion de contacts qui produisent une infection.

Face à une épidémie en phase montante, le fait même que l'épidémie se répande montre que le ${\displaystyle R_{0}}$ correspondant est significativement supérieur à l'unité. Les stratégies possibles consistent alors à accentuer les mesures sanitaires et sociales précédentes par des mesures exceptionnelles, ce qui permet de réduire le ${\displaystyle R_{0}}$ :

• Rechercher activement les personnes contagieuses, et les isoler en quarantaine obligatoire ;
• Appeler à une vigilance accrue en matière d'hygiène.

Observation directe

Le nombre de reproduction de base peut être estimé en examinant les chaînes de transmission détaillées, ou par séquençage génomique. Cependant, il est le plus souvent calculé à l'aide de modèles épidémiologiques^[10].

Mesure du ratio 0

Sur une courbe épidémiologique décrivant le nombre de nouveaux cas et tracée dans un repère semi-logarithmique, dans ce cas idéal, on verra dans un premier temps la courbe monter suivant une droite croissante (phase de croissance exponentielle), puis s'infléchir, et descendre suivant la pente inverse (phase de décroissance exponentielle). Comme discuté ci-dessous, il est possible d'estimer le ${\displaystyle R_{0}}$ à partir de la pente de la courbe.

• On peut théoriquement suivre, sur de telles courbes, l'effet de politiques de santé ayant pour effet de faire varier le ${\displaystyle R_{0}}$ à la suite de leur mise en application : l'effet sera en principe de diminuer la pente de la courbe, mais également de ralentir symétriquement la décroissance, et donc globalement d'étaler l'épidémie dans le temps.
• À partir de modélisations, il est théoriquement possible de calculer la hauteur du pic à partir du ${\displaystyle R_{0}}$, si l'on connaît la taille de la population concernée.

Il faut cependant être conscient que ce mécanisme, qui parle d'une « fraction ${\displaystyle f}$ de la population », ne peut suivre ce modèle que si la population a un périmètre défini, et est à la fois homogène, et isolée du reste du monde. Une immunité collective, acquise à l'échelle d'une région, peut néanmoins coïncider avec la contamination d'une région voisine non encore atteinte, déclenchant un nouveau pic de contamination à l'échelle nationale ; et dans ce cas, le signal du « pic » et sa symétrie théorique apparaîtront beaucoup plus brouillés par l'enchevêtrement des progressions géographiques.

Exemples de calcul

Le ${\displaystyle R_{0}}$ dépend de divers facteurs : région, comportements, densité de population, organisation sociale ou saisonnalité. Il ne s'agit donc pas d'une constante. Il est sujet à de nombreuses erreurs d'interprétation, et son calcul de ${\displaystyle R_{0}}$ se révèle difficile^[11].

Valeurs de R₀ pour des maladies communes^[12]

Maladie	Mode de transmission	R0
Rougeole	aérien	12–18
Coqueluche	aérien	12–17
Varicelle	aérien	10–12
COVID-19 - Variant Omicron	aérien	~10 [13]–12 à 15[14]
COVID-19 - Variant Delta	aérien	7,5 (J-F Delfraissy) [15]
Diphtérie	contact (salive)	6–7
Variole	contact	5–7
Polio	contact (matière fécale)	5–7
Rubéole	aérien	5–7
Oreillons	aérien	4–7
VIH/SIDA	contact (sang, sperme, sécrétions vaginales)	2–5[16]
Syndrome respiratoire aigu sévère	aérien	2–5[17]
Grippe (grippe espagnole de 1918)	aérien	2–3[18]
COVID-19 (souche d'origine)	aérien et contact	2-4

Caractère fluctuant du ratio 0

Le ${\displaystyle R_{0}}$ est un concept utile pour ce qui est du raisonnement qualitatif, mais il serait illusoire d'en attendre une mesure précise et stable dans une situation donnée.

En effet, la « transmissibilité » varie suivant les conditions des rencontres, et est extrêmement difficile à évaluer quantitativement même en conditions standardisées. Elle varie également suivant les conditions saisonnières : un agent pathogène qui prospère dans les conditions froides et humides, comme la grippe « saisonnière », voit son efficacité s'effondrer en été, diminuant d'autant le ${\displaystyle R_{0}}$.

De son côté, le « taux de contact » est extrêmement variable suivant le caractère sociable ou non du porteur (solitaire ou serveur de bar ?) ou du groupe social dans lequel il s'insère (club échangiste ou société d'Amish face à une MST). Il doit de plus prendre en compte la connectivité d'un groupe social à l'autre : une épidémie aviaire se transmettra très rapidement dans une même volière, mais les contacts d'une volière à une autre sont beaucoup plus limités. Enfin, il variera dans des proportions drastiques en cas d'épidémie importante, du seul fait de la variation des comportements : quand pendant les grandes épidémies de choléra les villageois accueillaient les étrangers à coup de fourche, la capacité d'un porteur à contaminer cette population s'en trouvait très diminuée.

Les discussions sur ce paramètre ${\displaystyle R_{0}}$ doivent donc être comprises comme des analyses essentiellement qualitatives, et les valeurs citées comprises comme des ordres de grandeurs plutôt que des seuils scientifiquement déterminés.

Ratio 0 et modélisation épidémiologique

Vitesse de croissance de l'épidémie

Pendant une épidémie, généralement le nombre d'infections diagnostiquées ${\displaystyle N(t)}$ au fil du temps ${\displaystyle t}$ est connu. Aux premiers stades d'une épidémie, la croissance est exponentielle en ${\displaystyle N(t)=e^{K.t}}$, avec un taux de croissance logarithmique ${\displaystyle K}$ tel que :

${\displaystyle K:={\frac {d\ln(N)}{dt}}\approx {\frac {\Delta \ln(N)}{\Delta t}}}$

Dans un repère semi-logarithmique, la courbe correspondante est une droite (aux fluctuations et erreurs de comptage près). Inversement, dans un tel tracé, à chaque fois que la courbe du nombre de nouveaux cas tend à être une droite, cela implique que le ${\displaystyle R_{0}}$ sous-jacent est resté constant, et donc qu'il n'y a pas eu de modification sensible à cette échelle du comportement général ou de la politique de santé.

Pour une croissance exponentielle, en début d'épidémie (où tout part d'une valeur négligeable), ${\displaystyle N}$ peut être interprété indifféremment comme le nombre cumulé de diagnostics (y compris les individus qui se sont rétablis) ou le nombre actuel de cas d'infection ; le taux de croissance logarithmique est le même pour l'une ou l'autre définition. En pratique, en début d'épidémie, la lecture est plus sûre sur le nombre cumulé de cas, qui porte sur des quantités plus importantes et a de ce fait des fluctuations moins importantes. En revanche, pour apprécier des pentes instantanées en cours d'épidémie, la mesure n'est généralement possible que sur le nombre de nouveaux cas.

Lien avec l'évolution temporelle

Les segments en droite ligne constatés dans un repère semi-logarithmique permettent de donner une première estimation du ${\displaystyle R_{0}}$.

Après la contamination initiale du sujet de base, les personnes contaminées le sont « en moyenne » après un temps ${\displaystyle \theta }$, qui dépend du temps d'incubation et de la durée de la période de contamination, et éventuellement du caractère plus ou moins contagieux en début ou en fin de cette période. Si l'on fait par exemple l'hypothèse simplificatrice que la contagiosité est uniforme sur la période, le délai moyen ${\displaystyle \theta }$ de contamination au rang 1 sera celui séparant la contamination initiale du milieu de la période contaminante.

D'un rang à l'autre les délais de contamination seront de plus en plus étalés, mais la loi des grands nombres fait que le délai moyen de contamination au rang ${\displaystyle n}$ sera alors ${\displaystyle n.\theta }$, c'est-à-dire ${\displaystyle n}$ fois le délai moyen au premier rang. Inversement, au bout d'un temps ${\displaystyle t}$, le rang atteint sera en moyenne le rang ${\displaystyle n=t/\theta }$.

En reportant cette valeur dans la loi de croissance du nombre de cas, le nombre ${\displaystyle N(t)}$ de nouvelles contaminations au bout d'un temps ${\displaystyle t}$ sera :

${\displaystyle N(t)=N_{0}.(R_{0})^{n}=N_{0}.e^{t.\ln(R_{0})/\theta }}$

On a donc :

${\displaystyle K=Ln(R_{0})/\theta }$, ou inversement : ${\displaystyle R_{0}=e^{\theta .K}}$

C'est cette dernière formule qui permet de mesurer le ${\displaystyle R}$ effectif, à partir de la pente ${\displaystyle K}$ du nombre de cas nouveaux, et du délai moyen de contamination ${\displaystyle \theta }$.

Temps de doublement

En croissance exponentielle, ${\displaystyle K}$ est lié au temps de doublement ${\displaystyle t_{2}}$ comme

Le ${\displaystyle R_{0}}$, nombre sans dimension, ne dit rien, par lui-même, sur le temps de doublement d'une maladie, qui a la dimension d'un temps. Clairement, si une personne en contamine deux en moyenne, le temps de doublement sera beaucoup plus bref si la durée d'incubation et la période de contamination sont courtes, et sera du même ordre de grandeur que celles-ci.

Afin d'estimer ${\displaystyle R_{0}}$, des hypothèses sont nécessaires sur le délai ${\displaystyle \delta _{0}}$ entre l'infection et le début de la contamination, et la durée ${\displaystyle \delta _{c}}$ de la période contaminante. Si l'on suppose pour simplifier qu'un malade est uniformément contagieux d'un bout à l'autre de sa période contaminante, le délai moyen de contamination pour le premier « rang » qu'il contamine est le milieu de cet intervalle de temps, soit : ${\displaystyle \delta _{0}+\delta _{c}/2}$, et dans ce cas, le délai moyen de contamination sera : ${\displaystyle \theta =\delta _{0}+\delta _{c}/2}$

On en déduit le temps de doublement ${\displaystyle t_{2}}$ par la formule d'évolution précédente :

${\displaystyle 2=e^{t_{2}.\ln(R_{0})/\theta }}$, soit encore : ${\displaystyle t_{2}=\theta .{\frac {\ln(2)}{\ln(R_{0})}}}$

Vitesse de récession de l'épidémie

Lorsque la vague épidémique s'apaise, le seuil d'immunité collectif ${\displaystyle P=1-1/R_{0}}$ a été franchi, et le ${\displaystyle R}$ effectif est devenu inférieur à l'unité. En queue d'épidémie, ce nombre de reproduction (qui dépend de la proportion ${\displaystyle p}$ de la population touchée et devenue immunisée) est sensiblement constant, et « toutes choses égales par ailleurs », on peut calculer le lien théorique entre ce nombre ${\displaystyle R_{1}}$ et le ${\displaystyle R_{0}}$ initial :

${\displaystyle R_{1}=(1-p).R_{0}}$ ;

La décroissance est alors exponentielle. Tracée dans un repère semi-logarithmique, la pente correspondante de la courbe est alors :

${\displaystyle K_{1}={\frac {\ln[(1-p).R_{0}]}{\theta }}}$

Pour de petites valeurs de ${\displaystyle R_{0}}$, et toutes choses égales par ailleurs :

• La somme des pentes ascendante et descendante est du second ordre, donc ces deux pentes sont sensiblement symétriques l'une de l'autre ;
• Cette somme tend à être négative, donc l'épidémie décroît plutôt plus vite qu'elle n'a crû.

C'est ce qui permet de dire que pour les faibles épidémies, la courbe des cas cumulés est sensiblement une sigmoïde. Pour les épidémies sévères, la population tend à modifier ses comportements entre-temps, changeant de ce fait la valeur du ${\displaystyle R_{0}}$, et il n'y a plus de raison que cette symétrie puisse être observée.

En dehors de tels pics symétrique, l'interprétation est inversement que ces conditions de son apparition n'ont en tout cas pas été remplies : la population exposée ne l'a pas été de manière homogène dans l'espace ou dans le temps, ou les mesures sanitaires ou sociales ont été modifiées, induisant un changement dans la progression de la courbe.

Notes et références

Bibliographie

• Bacaër N., « Mathématiques et épidémies », Cassini, 2021.
• « Covid-19 : une quatrième vague, "différente" des précédentes, pourrait arriver à la rentrée », Midi libre,‎ 9 juin 2021 (lire en ligne)
• « Covid-19 : l'arrivée d'Omicron peut-elle relancer le débat sur l'immunité collective ? », TV5 Monde,‎ 31 décembre 2021 (lire en ligne)

Voir aussi

• Modèles compartimentaux en épidémiologie (définition)
• Superinfecteur (définition)
• Diamond Princess (navire de croisière) (exemple)

• Portail de la médecine
• Portail des probabilités et de la statistique