Direkt limesz (kategóriaelmélet)

A matematikában a direkt limesz objektumok irányított rendszerének kategóriaelméleti értelemben vett kolimesze. Először adott algebrai struktúrák (pl. csoportok, modulusok) direkt limeszét definiáljuk, majd teljes általánosságban tetszőleges kategóriában is definiáljuk a direkt limesz fogalmát.

Definíciók

Algebrai objektumok

Ebben a szakaszban objektumaink algebrai struktúrával ellátott halmazok – például csoportok, gyűrűk, adott gyűrű fölötti modulusok, adott test fölötti algebrák, stb. Ennek szellemében „homomorfizmus” alatt mindig a megfelelő algebrai struktúrák közti homomorfizmust értjük, azaz például csoportok esetében csoporthomomorfizmust, gyűrűk esetében gyűrűhomomorfizmust s így tovább.

Először objektumok és homomorfizmusok direkt rendszerét definiáljuk. Ehhez tekintsünk egy ${\displaystyle \langle I,\leq \rangle }$ irányított halmazt: ez egy ${\displaystyle \leq }$ részbenrendezéssel ellátott ${\displaystyle I\,}$ halmaz úgy, hogy ${\displaystyle I\,}$ bármely két elemének létezik felső korlátja, azaz

${\displaystyle \forall i,j\in I:\,\exists k\in I:\,i\leq k,\,j\leq k}$.

Legyen ${\displaystyle \{A_{i}:i\in I\}}$ algebrai objektumok egy családja, ahol ${\displaystyle I\,}$ irányított indexhalmaz és minden ${\displaystyle i\leq j}$-re adott egy ${\displaystyle f_{ij}:A_{i}\rightarrow A_{j}}$ homomorfizmus az alábbi tulajdonságokkal:

1. ${\displaystyle f_{ii}\,}$ az ${\displaystyle A_{i}\,}$ identitása, valamint
2. ${\displaystyle f_{ik}=f_{jk}\circ f_{ij}}$ fennáll minden ${\displaystyle i\leq j\leq k}$ esetén.

Ekkor az ${\displaystyle \langle A_{i},f_{ij}\rangle }$ párt ${\displaystyle I\,}$ fölötti direkt rendszernek nevezzük.

Az ${\displaystyle \langle A_{i},f_{ij}\rangle }$ direkt rendszer direkt limeszének ${\displaystyle A\,}$ alaphalmazát az ${\displaystyle A_{i}\,}$ halmazok diszjunkt uniójának az alábbi ${\displaystyle \sim \,}$ ekvivalenciareláció szerinti faktoraként definiáljuk:

${\displaystyle A=\varinjlim A_{i}=\bigsqcup _{i}A_{i}{\bigg /}\sim .}$

Itt ${\displaystyle x_{i}\in A_{i}}$ és ${\displaystyle x_{j}\in A_{j}}$ ekvivalensek, jelölésben ${\displaystyle x_{i}\sim \,x_{j}}$, ha van olyan ${\displaystyle k\in I}$, melyre ${\displaystyle f_{ik}(x_{i})=f_{jk}(x_{j})\,}$. Heurisztikusan két elem akkor és csak akkor esik egybe a direkt limeszben, ha egy idő után a direkt rendszerben is egybeesnek. Az így definiált ${\displaystyle A\,}$ halmazt ugyanazzal a struktúrával látjuk el, amit a direkt rendszer elemei birtokoltak; a vonetkozó algebrai műveleteket értelemszerűen definiáljuk a reprezentánsokon. Például gyűrűk esetén az összeadás ${\displaystyle [x_{i}]+[x_{j}]:=[f_{ik}(x_{i})+f_{jk}(x_{j})]}$ lesz.

Ebből a definícióból azonnal adódik, hogy minden ${\displaystyle i\in I}$ indexre létezik egy ${\displaystyle \phi _{i}:A_{i}\rightarrow A}$ kanonikus morfizmus, ami minden elemhez az ${\displaystyle A\,}$-beli ekvivalenciaosztályát rendeli.

Fontos megemlíteni, hogy egy gyűrű feletti modulusok kategóriájában a direkt limesz egzakt funktor.

Direkt rendszer direkt limesze tetszőleges kategóriában

A direkt limeszt tetszőleges ${\displaystyle {\mathcal {C}}}$ kategóriában is definiálhatjuk egy megfelelő univerzális tulajdonság segítségével. ${\displaystyle {\mathcal {C}}}$-beli objektumok és morfizmusok direkt rendszere ugyanúgy definiálható, mint fent. Az ${\displaystyle \langle X_{i},f_{ij}\rangle }$ direkt rendszer direkt limesze az ${\displaystyle \langle X,\phi _{i}\rangle }$ pár, ahol ${\displaystyle X\,\in Ob\,{\mathcal {C}}}$, a ${\displaystyle \phi _{i}:X_{i}\rightarrow X}$ kanonikus morfizmusokkal együtt, melyekre ${\displaystyle \phi _{i}=\phi _{j}\circ f_{ij}}$ teljesül minden ${\displaystyle i,j\in I\,}$ esetén.

Az ${\displaystyle \langle X,\phi _{i}\rangle }$ pár univerzális abban az értelemben, hogy minden más ugyanezen feltételeknek eleget tevő ${\displaystyle \langle Y,\psi _{i}\rangle }$ párra egyértelműen létezik egy ${\displaystyle u:X\rightarrow Y}$ morfizmus, amely az alábbi diagramot minden ${\displaystyle i,j\in I\,}$-re kommutatívvá teszi:

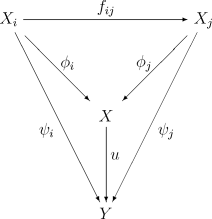
A direkt limeszt az alábbi módon jelölik:

${\displaystyle X=\varinjlim X_{i}}$

ahol a direkt rendszer továbbra is ${\displaystyle \langle X_{i},f_{ij}\rangle }$.

Az algebrai objektumok esetével ellentétben nem minden kategóriában létezik direkt limesz. Ha viszont létezik, akkor egyértelmű abban az erős értelemben, hogy ha ${\displaystyle X}$ és ${\displaystyle X*}$ is direkt limesze ugyanannak a direkt rendszernek, akkor egyértelműen létezik egy ${\displaystyle X*\,\to X\,}$ izomorfizmus, ami a kanonikus morfizmusokkal kommutál.

Itt jegyezzük meg, hogy egy ${\displaystyle {\mathcal {C}}}$ kategóriabeli direkt rendszer funktorokkal is leírható. Tetszőleges ${\displaystyle \langle I,\leq \rangle }$ irányított halmaz tekinthető ${\displaystyle {\mathcal {I}}}$ kis kategóriának, ahol a morfizmusok az ${\displaystyle i\rightarrow j}$ nyilakból állnak: ${\displaystyle i\rightarrow j}$ akkor és csak akkor, ha ${\displaystyle i\leq j}$. A direkt rendszer nem más, mint egy ${\displaystyle {\mathcal {I}}\rightarrow {\mathcal {C}}}$ kovariáns funktor.

Általános definíció

Legyenek ${\displaystyle {\mathcal {I}}}$ és ${\displaystyle {\mathcal {C}}}$ kategóriák. Jelölje ${\displaystyle c_{X}:{\mathcal {I}}\rightarrow {\mathcal {C}}}$ az ${\displaystyle X\in Ob{\mathcal {C}}}$-be menő konstans funktort. Tetszőleges ${\displaystyle F:{\mathcal {I}}\rightarrow {\mathcal {C}}}$ funktorhoz definiáljuk a

${\displaystyle \lim _{\longrightarrow }F:{\mathcal {C}}\rightarrow \mathbf {Set} }$

funktort, amely minden ${\displaystyle X\in Ob{\mathcal {C}}}$ objektumhoz a ${\displaystyle F\to c_{X}}$ természetes transzformációk ${\displaystyle \mathrm {Hom} (F,c_{X})}$ halmazát rendeli. Ha ${\displaystyle \lim _{\longrightarrow }F}$ reprezentálható, akkor a ${\displaystyle {\mathcal {C}}}$-beli reprezentáns objektumot F direkt limeszének nevezzük és szintén ${\displaystyle \lim _{\longrightarrow }F}$-fel jelöljük.

Legyen a ${\displaystyle {\mathcal {C}}}$ kategória Abel, ahol objektumok tetszőleges (akár végtelen) direktösszege létezik (ez az AB3 Grothedieck axióma ). Ekkor a ${\displaystyle \lim _{\longrightarrow }F}$ funktor reprezentálható minden ${\displaystyle F:{\mathcal {I}}\rightarrow {\mathcal {C}}}$ funktorra és

${\displaystyle \lim _{\longrightarrow }:\mathrm {Hom} ({\mathcal {I}},{\mathcal {C}})\rightarrow {\mathcal {C}},F\mapsto \lim _{\longrightarrow }F}$

Abel kategóriák közti jobbegzakt funktor.

Példák

• Egy M halmaz ${\displaystyle M_{i}}$ részhalmazainak egy családján a tartalmazás részbenrendezés. Direkt limesze az unió: ${\displaystyle \bigcup M_{i}}$.
• Let I be tetszőleges irányított halmaz, amelynek van legnagyobb eleme, legyen ez m. Ekkor a megfelelő direkt rendszer direkt limesze izomorf X_m-mel, a φ_m: X_m → X kanonikus morfizmus izomorfizmus.
• Legyen p prímszám. Tekintsük a Z/pⁿZ csoportok és a p-vel való szorzás által indukált Z/pⁿZ → Z/pⁿ⁺¹Z homomorfizmusok direkt rendszerét. Ennek a rendszernek a direkt limesze az összes p-hatvány rendű egységgyök által alkotott Z(p^∞) csoport.
• A direkt limesz és az inverz limesz kapcsolata:

${\displaystyle \mathrm {Hom} (\varinjlim X_{i},Y)=\varprojlim \mathrm {Hom} (X_{i},Y).}$

• Tekintsük az {A_n, φ_n} sorozatot, ahol A_n C*-algebra és φ_n : A_n → A_{n + 1} *-homomorfizmus. A direkt limesz konstrukciójának C*-analogonja a fenti univerzális tulajdonságot kielégítő C*-algebra.

Kapcsolódó konstrukciók és általánosítások

A direkt limesz kategóriaelméleti értelemben vett duálisa az inverz limesz. Általánosabb kategóriaelméleti fogalmak a limesz és a kolimesz. Az elnevezések megtévesztők lehetnek: a direkt limesz kolimesz, míg az inverz limesz limesz.

Hivatkozások

• Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from the French, Paris: Hermann, MR0237342
• Mac Lane, Saunders (1998), Categories for the Working Mathematician, vol. 5 (2nd ed.), Graduate Texts in Mathematics, Springer-Verlag